Hamarosan kiderült, hogy a hullámvezetõ módusai érzékenyen függenek a felületi viszonyoktól. Ez tette lehetõvé a sík hullámvezetõk alkalmazását mint optikai felületi szenzorokat. Molekulák adszorpciója és deszorpciója, vagy más törésmutató változás a hullámvezetõ felületén megváltoztatja az effektív törésmutatót és így a becsatolási szöget. Ez a szög nagy pontossággal mérhetõ, mely lehetõvé teszi a felületi változások követését (optikai hullámvezetõ módus spektroszkópia). A módszert sikeresen alkalmazták a fehérje-adszorpció kinetikájának tanulmányozására, lipid kettõsrétegek vizsgálatára (pl. gyógyszer beépülés). A mérés során a sík optikai hullámvezetõk egyszerûsített elvével és alkalmazásával ismerkedhetünk meg.
Tehát elegendõen nagy beesési
szöggel rendelkezõ sugarak teljes visszaverõdéssel
terjedhetnek a film közegében. Azonban a filmben terjedõ
sugarak között interferencia lép fel és csak azon
sugarak terjedhetnek, melyek erõsítik egymást. A kétszeres
teljes visszaverõdés után (A és C-nél,
l. 1. ábra) a C-nél lévõ sugár AC-AB=2dF
cos![]() úthosszal
késik az A-nál lévõ sugárhoz képest.
Ezen kívül fázistolások lépnek fel a teljes
visszaverõdésnél (
úthosszal
késik az A-nál lévõ sugárhoz képest.
Ezen kívül fázistolások lépnek fel a teljes
visszaverõdésnél (![]() 1
és
1
és ![]() 2
az SF és az FC határfelületeknél). A fázistolásokat
az un. Fresnel egyenletek adják meg és függenek a beesési
szögtõl és a három közeg törésmutatóitól.
2
az SF és az FC határfelületeknél). A fázistolásokat
az un. Fresnel egyenletek adják meg és függenek a beesési
szögtõl és a három közeg törésmutatóitól.
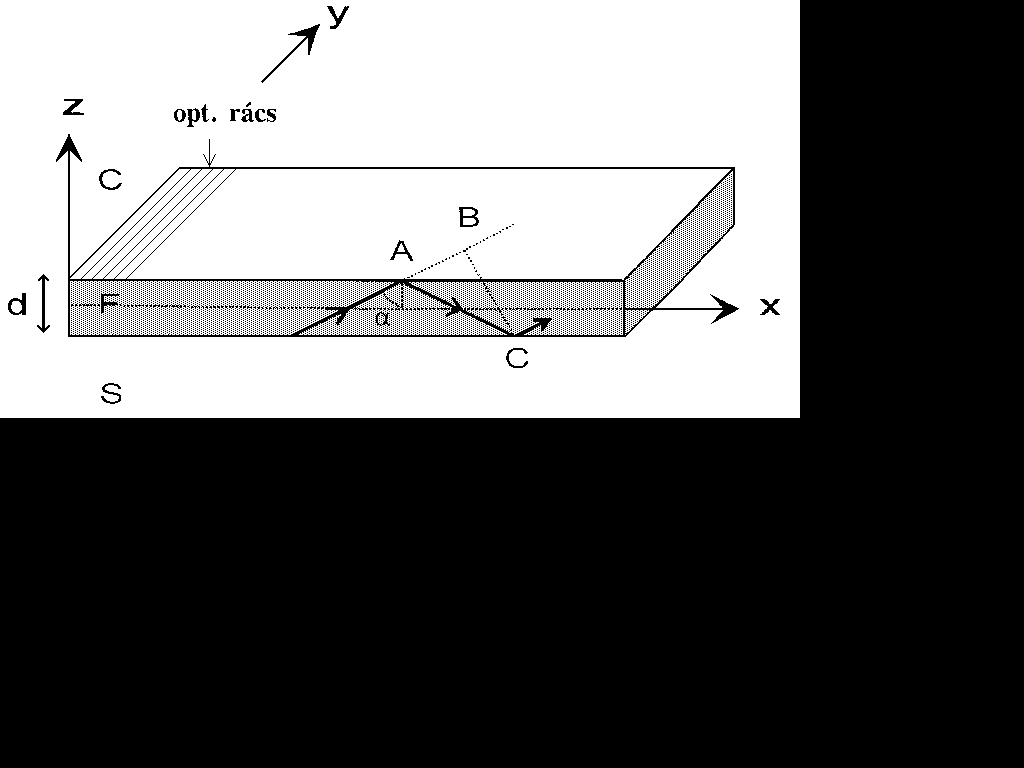
1. ábra. A hullámvezetõ film (F)
a két határoló közeggel (S és C). Teljes
visszaverõdés lép fel az SF és FC határfelületeknél.
A továbbiakban feltételezzük,
hogy a síkhullám az y irányban van polarizálva,
ekkor az elektromos tér y irányú, azaz a hullámvezetõ
módus tranzverz elektromos (TE). A tranzverz mágneses módus
(TM, a mágneses tér y irányú) hasonlóan
kezelhetõ. A hullámvezetõben terjedõ sugarakra
az erõsítés feltétele, hogy a két sugár
közötti teljes fázistolás a 2![]() egész számú (m=0, 1, 2,...) többszöröse
legyen:
egész számú (m=0, 1, 2,...) többszöröse
legyen:
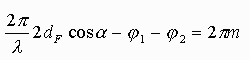
(Itt ![]() =
=![]() 0
/nF
a hullámhossz a hullámvezetõ filmben,
0
/nF
a hullámhossz a hullámvezetõ filmben, ![]() 0
pedig a vákuumban.) Ez az egyenlet a 3-rétegû sík
hullámvezetõ módus-egyenlete, m pedig a módus
szám. Átrendezve az egyenletet, kapjuk:
0
pedig a vákuumban.) Ez az egyenlet a 3-rétegû sík
hullámvezetõ módus-egyenlete, m pedig a módus
szám. Átrendezve az egyenletet, kapjuk:
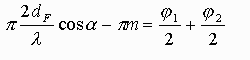
Ezen egyenlet bal oldala (BO) függ az ![]() beesési szögtõl, a film vastagságától
és törésmutatójától. Az egyenlet
jobb oldala (JO) az
beesési szögtõl, a film vastagságától
és törésmutatójától. Az egyenlet
jobb oldala (JO) az ![]() beesési szög és mindhárom közeg törésmutatóinak
függvénye. Az egyenlet két oldalát külön
ábrázoltuk a 2. ábrán a cos
beesési szög és mindhárom közeg törésmutatóinak
függvénye. Az egyenlet két oldalát külön
ábrázoltuk a 2. ábrán a cos![]() függvényében. (Itt jegyezzük meg, hogy az elektronikában
használatos chip elnevezéshez hasonlóan, a ráccsal
ellátott sík optikai hullámvezetõt szokás
optikai
chip-nek nevezni.) A 2. ábra vastag görbéihez az
ASI-2400 optikai chip paramétereit választottuk: nF
=
1,76, dF = 200 nm, nS = 1,5258, nC
= 1,333 (víz),
függvényében. (Itt jegyezzük meg, hogy az elektronikában
használatos chip elnevezéshez hasonlóan, a ráccsal
ellátott sík optikai hullámvezetõt szokás
optikai
chip-nek nevezni.) A 2. ábra vastag görbéihez az
ASI-2400 optikai chip paramétereit választottuk: nF
=
1,76, dF = 200 nm, nS = 1,5258, nC
= 1,333 (víz), ![]() 0
=
632,82 nm (He-Ne lézer fény). A két görbe metszése
(nyíl) megadja az egyedüli m=0 módust, mely ebben
a hullámvezetõben terjedni tud (
0
=
632,82 nm (He-Ne lézer fény). A két görbe metszése
(nyíl) megadja az egyedüli m=0 módust, mely ebben
a hullámvezetõben terjedni tud (![]() ~ 65,30 ). Ha a hullámvezetõ film vastagságát,
dF
-t 600 nm-re növeljük, akkor a hullámvezetõben
két módus tud terjedni: m= 0 és 1, melyeket
a 2. ábrán szaggatott vonalakkal ábrázoltunk.
(Vegyük figyelembe, hogy a film vastagságának növelésével
a fenti egyenletnek csak a bal oldala változik.) Érdekes
megjegyezni, hogy az egyenlet jobb oldala nem megy zérushoz, amint
cos
~ 65,30 ). Ha a hullámvezetõ film vastagságát,
dF
-t 600 nm-re növeljük, akkor a hullámvezetõben
két módus tud terjedni: m= 0 és 1, melyeket
a 2. ábrán szaggatott vonalakkal ábrázoltunk.
(Vegyük figyelembe, hogy a film vastagságának növelésével
a fenti egyenletnek csak a bal oldala változik.) Érdekes
megjegyezni, hogy az egyenlet jobb oldala nem megy zérushoz, amint
cos![]() -t növeljük.
A görbe megszakad amint
-t növeljük.
A görbe megszakad amint ![]() eléri a kritikus határszöget (~600 ) az SF
határfelületnél. Ez megad egy dF ~
91 nm "levágási" film vastagságot, mely alatt nem
terjedhet módus a hullámvezetõben (ennél a
hullámhossznál).
eléri a kritikus határszöget (~600 ) az SF
határfelületnél. Ez megad egy dF ~
91 nm "levágási" film vastagságot, mely alatt nem
terjedhet módus a hullámvezetõben (ennél a
hullámhossznál).
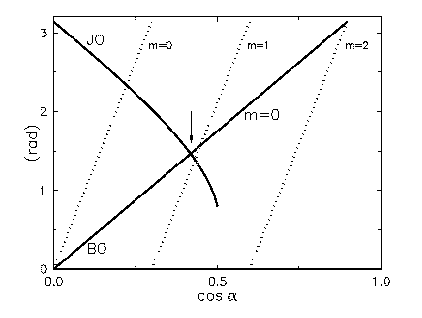
2. ábra. A módus kialakulása a hullámvezetõben
A hullámvezetõben a hullámszám vektor (k)
x-komponensét terjedési állandónak (![]() m
)
nevezik, melyet a következõ egyenlet ad meg:
m
)
nevezik, melyet a következõ egyenlet ad meg:
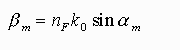
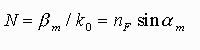
Növekvõ módus számmal (m) N csökken, míg a fázissebesség nõ.
A fény hullámvezetõbe történõ becsatolására rendszerint egy optikai rácsot alakítanak ki a hullámvezetõ filmen (1. ábra). A becsatolás feltételét a következõ egyenlet adja meg:
ahol l = 0, ±1,.... Itt n0 a levegõ
törésmutatója és ![]() 0
a
levegõben mért beesési szög (a z tengelyhez viszonyítva,
l. az 1. ábrát).
0
a
levegõben mért beesési szög (a z tengelyhez viszonyítva,
l. az 1. ábrát). ![]() az optikai rács állandója, azaz a vonalak közötti
távolság nm-ben. Az ASI-2400 optikai chip-re
az optikai rács állandója, azaz a vonalak közötti
távolság nm-ben. Az ASI-2400 optikai chip-re ![]() ~ 416,7 nm, mivel 2400 db vonal esik 1 mm-re. Rendszerint l =
±1 adja a becsatolást.
~ 416,7 nm, mivel 2400 db vonal esik 1 mm-re. Rendszerint l =
±1 adja a becsatolást.
A gyakorlatban általában négy réteget kell
figyelembe venni az optikai hullámvezetõnél. A negyedik
réteg lehet egy,a hullámvezetõ filmre felvitt kettõs
lipid réteg, vagy a filmre adszorbeált fehérje réteg.
(Ezeket a vékony rétegeket adlayer-nek nevezik.) Ekkor
a módus egyenlet bonyolultabbá válik, azonban numerikusan
megoldható.
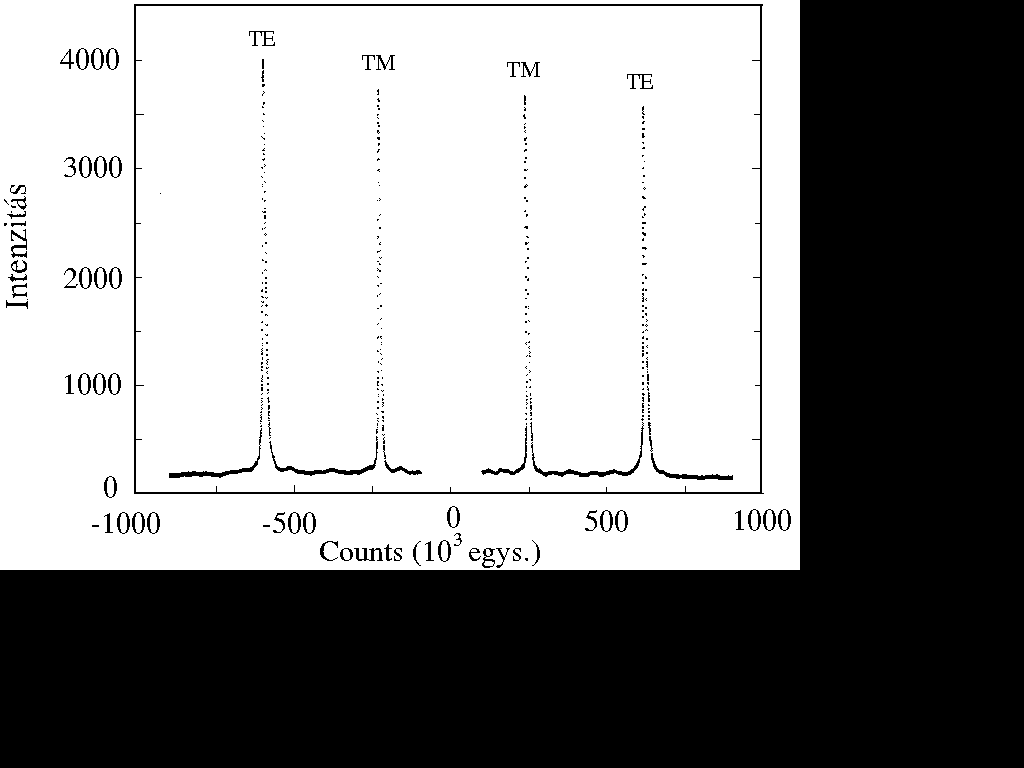
3. ábra. Hullámvezetõ módus spektrum.
Egy C nyelven írt program vezérli a
DC motort, a fotodiódák által mért fényintenzitást
adott lépésenként egy AD (analóg-digitál)
konverter digitalizálja, majd az adatokat egy PC tárolja.
Egy ilyen spektrumot a 3. ábra mutat. Mérés közben
a program görbe fittelést végez a maximum-helyek meghatározására,
kiszámítja az effektív törésmutatókat
és a képernyõn megjeleníti.A berendezés
tervezése, összeállításaés a szoftver
az ELTE, TTK, Biológiai FizikaTanszéken készült.
Ellenõrzõ fogalmak és kérdések:
- optikai törésmutató és a teljes visszaverõdés,
interferencia
- az optikai hullámvezetõk néhány alkalmazása
- az optikai hullámvezetõ felépítése
- fény terjedése a hullámvezetõben
- a hullámvezetõ módus fogalma, jellemzõi
- az interferencia szerepe a hullámvezetõ módus
kialakulásában
- egy módus effektív törésmutatója
- hullámvezetõ spektrum, TE és TM módusok
- jeldigitalizálás, AD konverterek